|
funcion polinomial
INGRID MUNIVE PEREZ
Una función polinomial de grado n con una variable es una expresión algebraica de la forma:
ƒ(x) = anxn + an-1xn-1 + an-2xn-2 + ... + a2x2 + a1x1 + a0
en la cual x es la variable y las an, an-1, etc. son los coeficientes. Se llama función porque para cualquier valor de x existe uno y solo un valor de ƒ(x).
Ejemplo. El polinomio x4 + x3 - 11x2 - 9x + 18 es de cuarto grado (por el exponente 4 de su primer término) y su indeterminada o variable es x. Con este polinomio se puede definir la función polinomial de grado 4 con una variable:
ƒ(x) = x4 + x3 - 11x2 - 9x + 18
FUNCIONES RACIONALES
se llama una función racional, donde Q(x) es diferente de cero.
Ejemplos:
El dominio de las funciones racionales es el conjunto de todos los números reales tal que el denominador sea diferente de cero.
Ejemplo para discusión: ¿Cuál es el dominio de cada una de las siguientes funciones?
Teorema: Sea f una función racional definida de la forma:
donde P(x) y Q(x) son polinomios. Si a es un número real que Q(a) = 0 y P(a) es diferente de cero, entonces la recta x = a es una asíntota vertical de la gráfica de y = f(x).
Ejemplos para discusión: Halla las asíntotas verticales para cada de las siguientes funciones:
Teorema: Sea f una función racional definida por el cociente de dos polinomios,
entonces:
1) Para m < n, la recta y = 0 (el eje x) es una asíntota horizontal.
2) Para m = n, la recta y = am/bn, es una asíntota horizontal.
3) Para m > n, no hay asíntotas horizontales.
Ejemplos para discusión: Halla las asíntotas horizontales para cada una de las siguientes funciones:
Gráfica de funciones racionales
Ahora utilizaremos las técnicas de interceptos y asíntotas para graficar algunas funciones racionales.
Ejemplos para discusión: Dibuja la gráfica de:
Ejercicio de práctica: Halla las asíntotas verticales y horizontales para cada una de las siguientes funciones. Dibuja la gráfica.
Teorema: Si f es una función definida de la forma:
donde P(x) y Q(x) son polinomios y el grado de P(x) es 1 más que el grado de Q(x), entonces se puede expresar de la forma:
donde el grado de r(x) es menor que el grado de Q(x). La recta y = mx + b es una asíntota oblicua para la gráfica de f.
Ejemplo para discusión: Halla las asíntotas verticales, horizontales y oblicuas para:
Dibuja la gráfica.
Ejercicio de práctica: Halla las asíntotas verticales, horizontales y oblicuas para:
Dibuja la gráfica.
|
macuarros de la construccion
jueves, 13 de junio de 2013
Diego Arturo Granillo Cabrera N.L 16
FUNCIÓN POLINOMIAL
¿Cuánto pagaremos?
x:
kg de manzanas que compramos
f(x):
precio que se paga en euros
f(x)=0,75x
Funciones de proporcionalidad directa
Las funciones polinómicas de primer grado con término
independiente cero, representan la relación entre dos variables directamente
proporcionales.
y=constante·x
La
gráfica de la función de proporcionalidad directa es una recta que pasa por el
origen, y su pendiente es la constante de proporcionalidad
FUNCIÓN
RACIONAL
¿Qué cantidad de aceite con contenido de 0.3% de azufre debe
mezclar un químico, en 100 litros con 0.6% de azufre para conseguir un aceite
que contenga 0.4%
m(x) = 0.006(100) + 0.003x
Luego, sustituyendo la mezcla deseada de
(100 + x) litros de 0.4% de azufre para m,
0.004(100 + x) = .006(100) + .003x
0.4 + .004x = 0.6 + .003x
0.001x = 0.2
x = 200
Luis Manuel Hidalgo Hernandez N.L 23
FUNCIÓN POLINOMIAL
x: kg de
naranjas que compramos
f(x):
precio que se paga en euros
f(x)=0,75x
Funciones de proporcionalidad directa
Las
funciones polinómicas de primer grado con término independiente cero,
representan la relación entre dos variables directamente proporcionales.
y=constante·x
FUNCIÓN
RACIONAL
¿Qué
cantidad de aceite con contenido de 0.5% de azufre debe mezclar un químico, en
100 litros con 0.8% de azufre para conseguir un aceite que contenga 0.6%
Solución:
Haciendo x = la cantidad de aceite de 0.5% para mezclar, tenemos
m(x)
= 0.008(100) + 0.005x
Luego,
sustituyendo la mezcla deseada de
(100
+ x) litros de 0.6% de azufre para m,
0.006(100
+ x) = .008(100) + .005x
0.6
+ .006x = 0.8 + .005x
0.001x
= 0.2
x = 200
martes, 11 de junio de 2013
Gráficas
de las funciones racionales (Aguilar Ramos juan Manuel )
Ejemplo 1
Las funciones racionales son del tipo:
El dominio de una función
racional de lo
forman todos los números reales menos los valores de x que anulan el denominador.
Ejemplo
Un
tipo de función racional es la función de
proporcionalidad inversa de ecuación:
Una función polinomio de grado n con una variable es una expresión
algebraica de la forma:
ƒ(x) =
anxn + an-1xn-1 + an-2xn-2 + ... + a2x2 + a1x1 + a0
en la cual x es la variable y las an, an-1, etc. son los coeficientes. Se llama
función porque para cualquier valor de x existe uno y solo un valor de ƒ(x).
Ejemplo. El polinomio x4 + x3 - 11x2 - 9x + 18 es de cuarto grado (por el exponente 4
de su primer término) y su indeterminada o variable es x. Con este polinomio se puede
definir la función polinomial de grado 4 con una variable:
ƒ(x) = x4 + x3 - 11x2 - 9x + 18
Evaluar
la función ƒ(x) = x4 + x3 - 11x2 - 9x + 18 cuando el valor numérico de x es (4)
ƒ(4) = 44 + 43 - 11(4)2 - 9(4) + 18
ƒ(4) = 256 + 64 - 11(16) - 36 + 18
ƒ(4) = 256 + 64 - 176 - 36 + 18
ƒ(4) = 126
Primero se evalúa numéricamente ƒ(x) para cada uno de los valores de x y se definen las coordenadas de cada uno de los puntos:
ƒ(4) = 44 + 43 - 11(4)2 - 9(4) + 18
ƒ(4) = 256 + 64 - 11(16) - 36 + 18
ƒ(4) = 256 + 64 - 176 - 36 + 18
ƒ(4) = 126
Primero se evalúa numéricamente ƒ(x) para cada uno de los valores de x y se definen las coordenadas de cada uno de los puntos:
|
x
|
ƒ(x)
|
(x, ƒ(x))
|
|
-4
|
70
|
(-4, 70)
|
|
-3
|
0
|
(-3, 0)
|
|
-2
|
0
|
(-2, 0)
|
|
-1
|
16
|
(-1, 16)
|
|
0
|
18
|
(0, 18)
|
|
1
|
0
|
(1, 0)
|
|
2
|
-20
|
(2, -20)
|
|
3
|
0
|
(3, 0)
|
|
4
|
126
|
(4, 126)
|
DIEGO GODOY LOZANO N°14 FUNCION RACIONAL
Calcula las asíntotas verticales y horizontales de la función 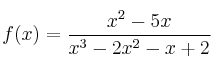
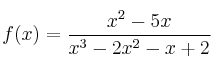
Solución:
Buscamos las asíntotas verticales en los puntos que anulan el denominador.
Resolvemos la ecuación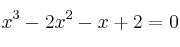 y obtenemos como soluciones
y obtenemos como soluciones 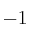 ,
, 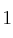 y
y 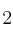 . Por tanto las asíntotas verticales son las rectas:
. Por tanto las asíntotas verticales son las rectas: 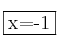 ,
, 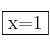 y
y 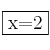
Asíntotas horizontales
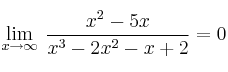 (porque el grado del denominador es mayor), por tanto tiene como asíntota horizontal la recta
(porque el grado del denominador es mayor), por tanto tiene como asíntota horizontal la recta 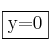
Resolvemos la ecuación
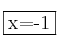 ,
, 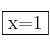 y
y 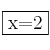
Asíntotas horizontales
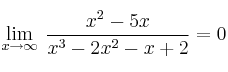 (porque el grado del denominador es mayor), por tanto tiene como asíntota horizontal la recta
(porque el grado del denominador es mayor), por tanto tiene como asíntota horizontal la recta 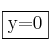
DIEGO GODOY LOZANO N° 14 FUNCION POLINOMICA
Ejemplo 1:
Encontrar las raíces de la funciónx = x 3 + 3 x 2 + 2 x
Solución:
Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos:
x = x x + 1 x + 2
Las raíces de la función x = x 3 + 3 x 2 + 2 x son x=0, x=-1 y x=-2
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
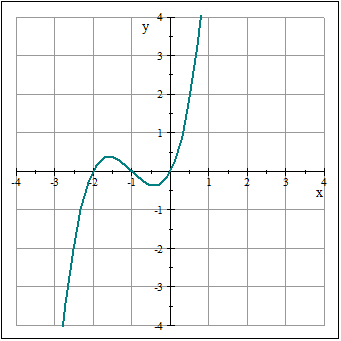
Ejemplo 2:
Encontrar las raíces de la funciónx = x 3 + 5 x 2 + 4 x
Solución:
Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos:
x = x x + 1 x + 4
Las raíces de la función x = x 3 + 5 x 2 + 4 x son x=0, x=-1 y x=-4
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
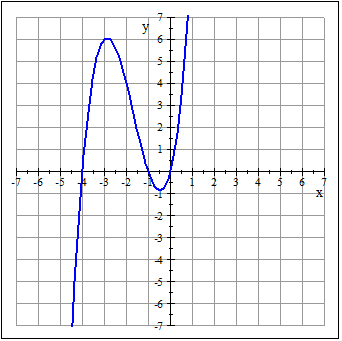
Encontrar las raíces de la función
Solución:
Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos:
o
|
o
|
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

Ejemplo 2:
Encontrar las raíces de la función
Solución:
Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos:
o
|
o
|
Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:

CYNTIA LOPEZ CARRASCO N°24 FUNCION POLINOMIAL Y RACIONAL
PLOBLEMA
DE FUNCION RACIONAL
Encontrar las asíntotas de la siguiente función:
Encontrar las asíntotas de la siguiente función:
Solución: Asíntotas verticales:
El valor x = 2, es una
raíz
del denominador pero no del numerador, por lo
tanto
es una asíntota vertical.
Asíntotas horizontales:
puesto que el denominador
tiene
el mismo grado que el numerador, la recta y = 4
es una asíntota horizontal. Ver la grafica de la
derecha.
PROBLEMA DE FUNCION
POLINOMIAL
1.-Cierta compañía ofrece un móvil
rebajado según puntos conseguidos tal
como indica la tabla, ¿corresponde esta
tabla a una función polinómica de
primer grado?. En caso afirmativo ¿cuál
es la ecuación?
Puntos (x) : 3000 5000 6000
Precio €(y): 220 200 190
R= y=-0,01x+250
2.-Al lanzar verticalmente hacia arriba un
R= y=-0,01x+250
2.-Al lanzar verticalmente hacia arriba un
objeto, con velocidad inicial 24 m/seg la
altura máxima que alcanza viene dada
por: f(x)=24x-5x2 (g=10 m/seg2 y
x:tiempo).
Calcula
la altura máxima que alcanza.
R= 28,8 m
R= 28,8 m
Suscribirse a:
Entradas (Atom)













